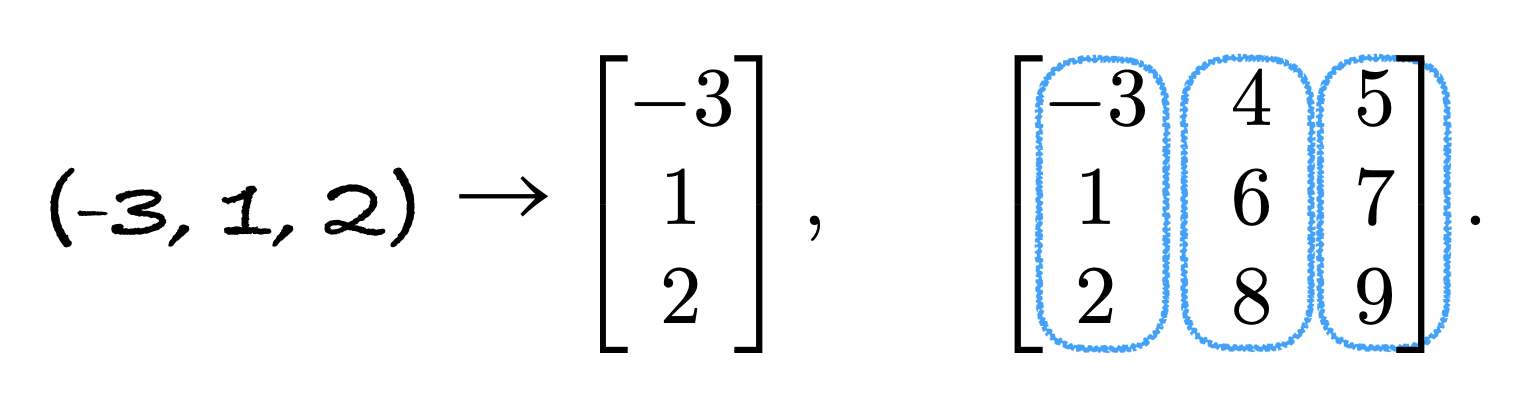【Unity】同次座標系をマスターしよう -「w」の正体まで徹底図解！
Computer Graphics (CG)の世界でマスターしておきたい、でもなかなか手をつけにくい、、、それが同次座標系です。
3次元空間でのオブジェクトは、拡大・縮小、回転、平行移動を組み合わせることで編集することができます。そして、同時座標系を用いれば、そうした操作を行列の掛け算だけで実現することができるのです。
今回は、座標、ベクトル・行列といった基礎的な内容を出発地点として、行列の掛け算とオブジェクトの操作を視覚的に捉えた後、xyzの次に来る「w」の正体に迫っていきます。
座標とは？
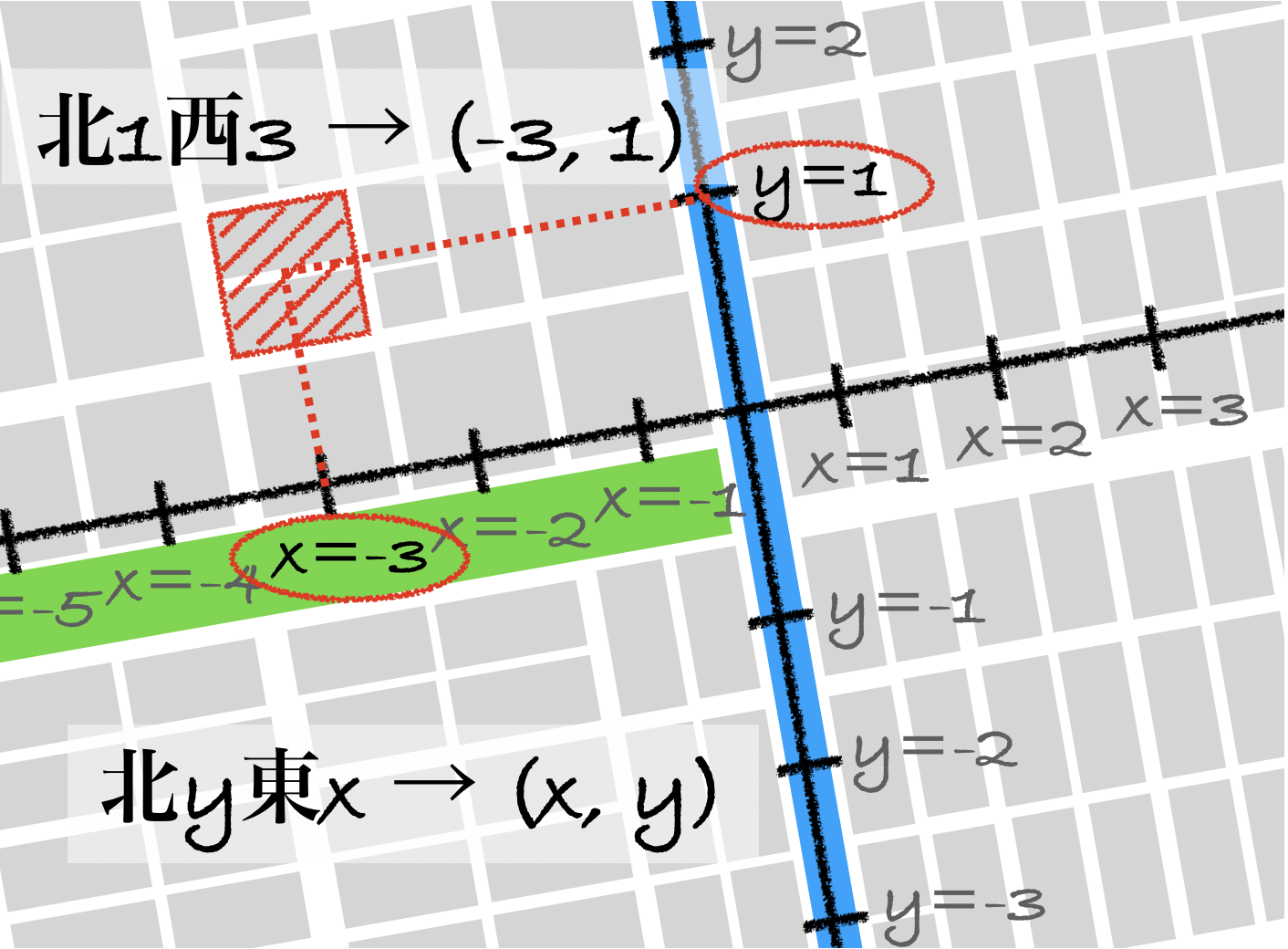
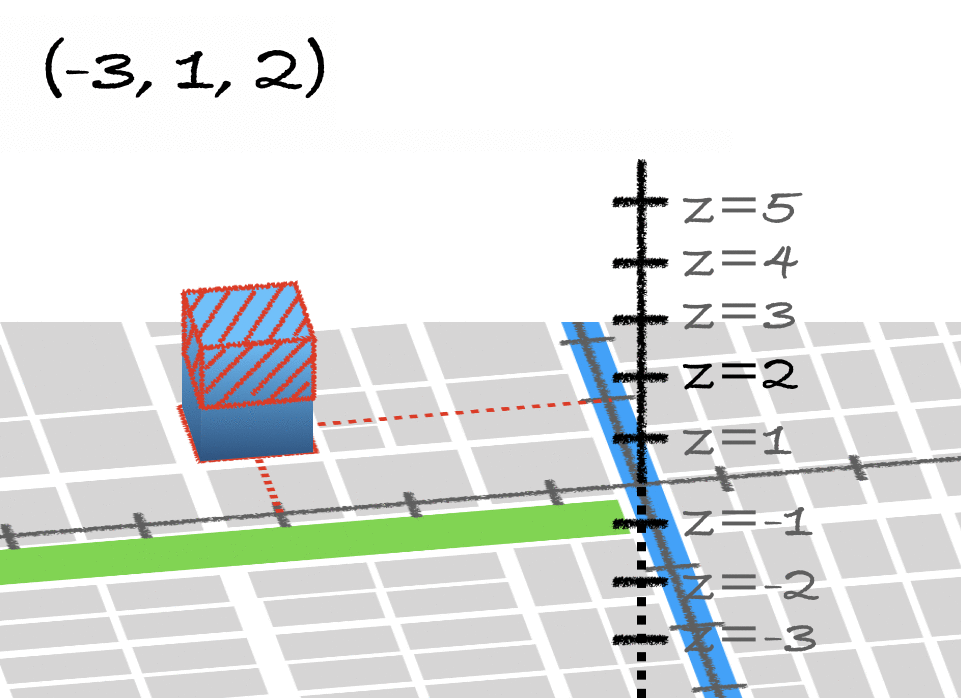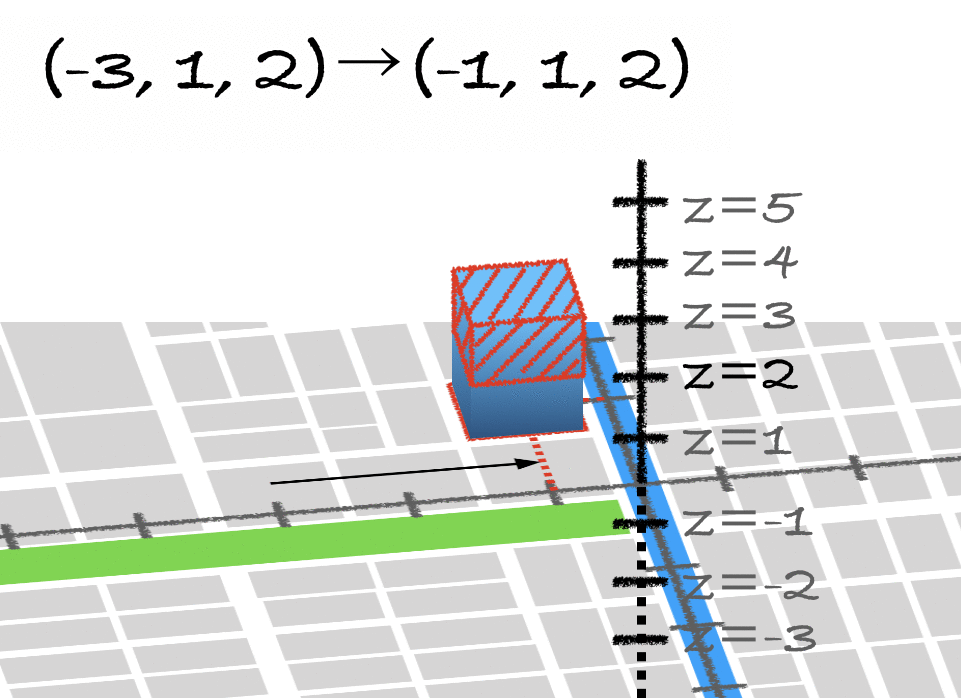
座標を一言で例えると、それは住所です。札幌市の碁盤目状の区画を見てみましょう。
札幌市の住所は、方角と2つの数字から出来ています。つまり、大通り公園と創成川からどの方向にどれだけ離れているかが分かれば、自分の現在地を把握できるのです。
大通り公園・創成川をx軸・y軸に置き換えれば、住所はすぐさま座標となります。マイナスの数字も許してあげましょう。すると、2次元平面での座標は、2つの数字で表すことができることに気付きます。
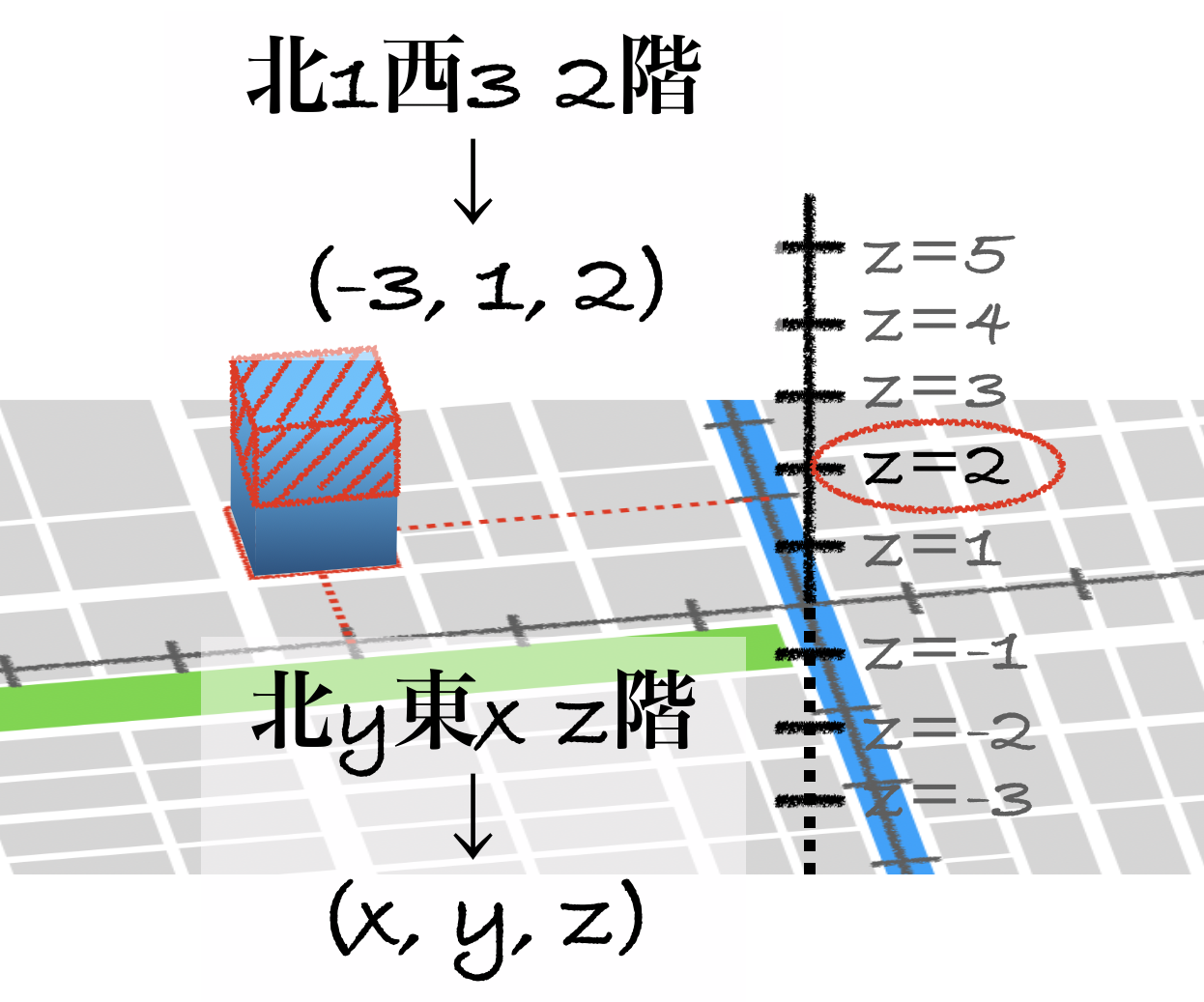
同様にして、3次元空間での座標は、3つの数字で表すのです。これが直交座標（xyz座標）です。
※Unityは左手系を採用しているため、上の図と軸の向きが異なります。その辺りは、以下の記事をご参照ください。
（関連記事：【Unity】Quaternionでオブジェクトを回転させる方法）
ベクトルと行列
先ほどの座標を、1列に並べて書くことにしましょう。これがベクトルです。ベクトルを並べると、それが行列となります。
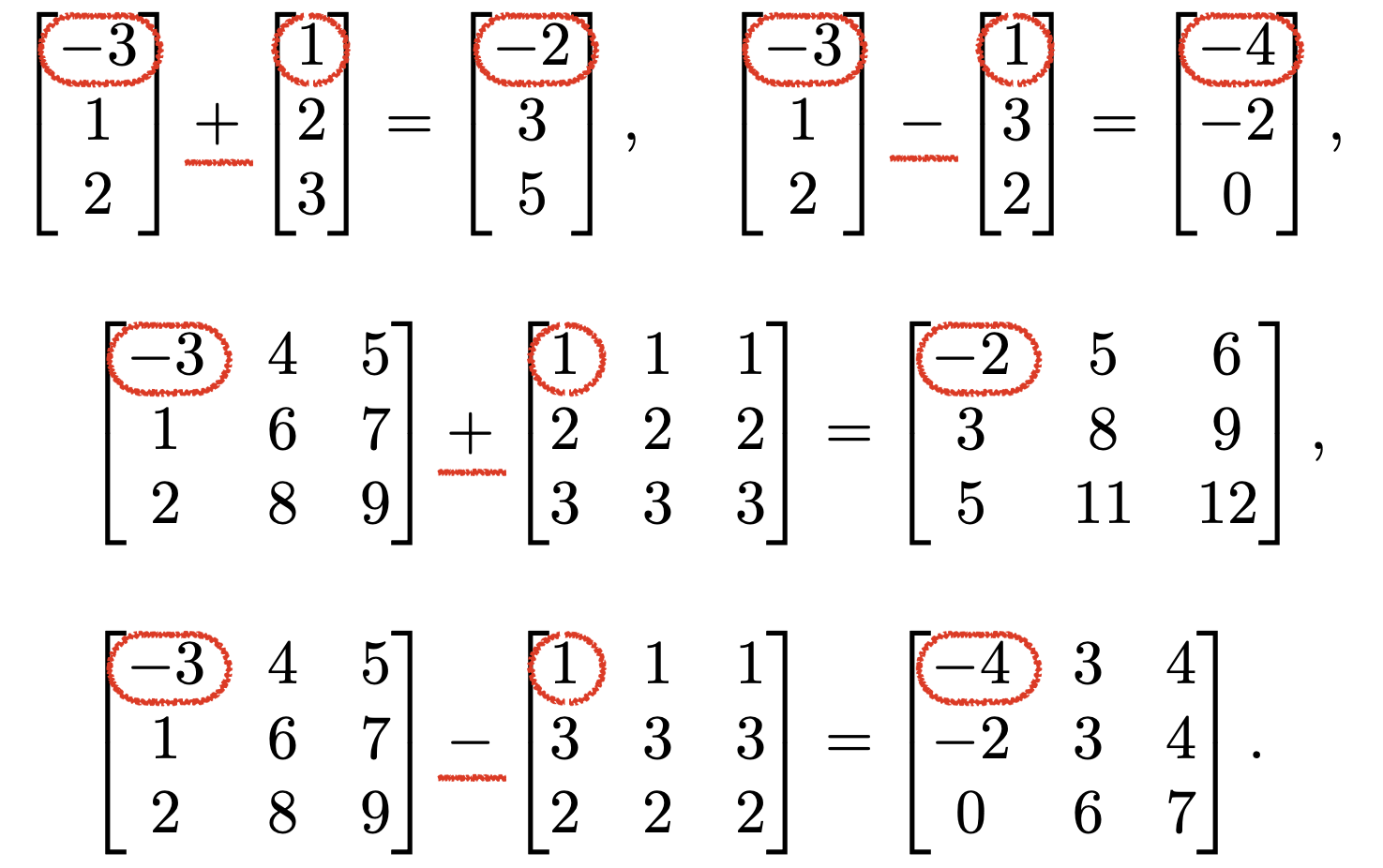
足し算と引き算
ベクトル・行列の足し算と引き算は、下のように、同じ場所にある数を各々計算します。
掛け算
掛け算は少しトリッキーです。下のように、同じ色で囲われた数を先ず掛け、その結果を合計します。
※ベクトルを1列に書いても、1行に書いても、本質的な違いはありません。但し、掛け算の順序に注意しましょう！
※ベクトル・行列の掛け算では、順序が重要です。掛ける順番が違えば、結果も違ってしまいます。
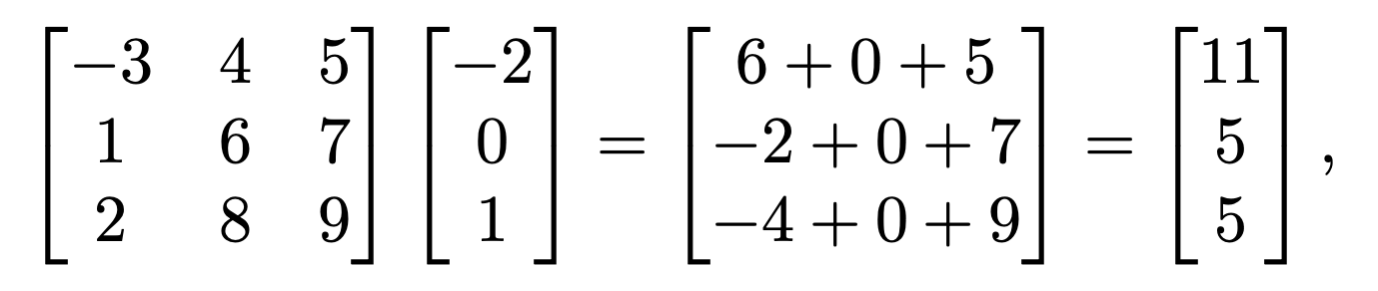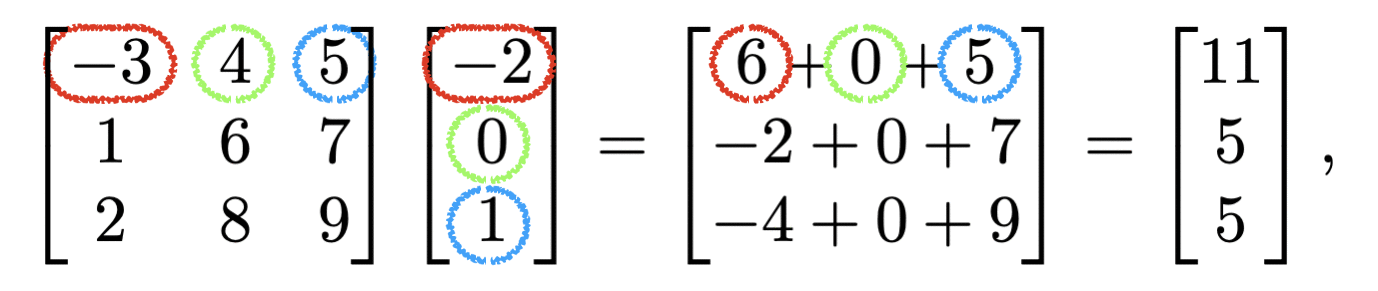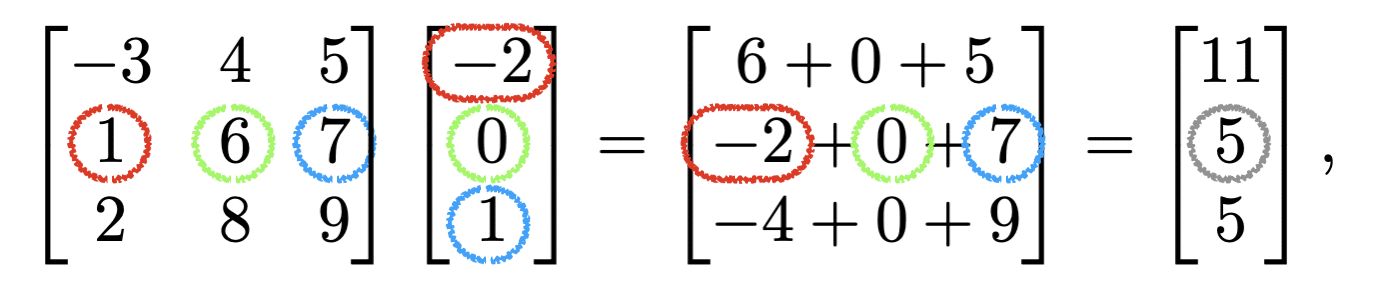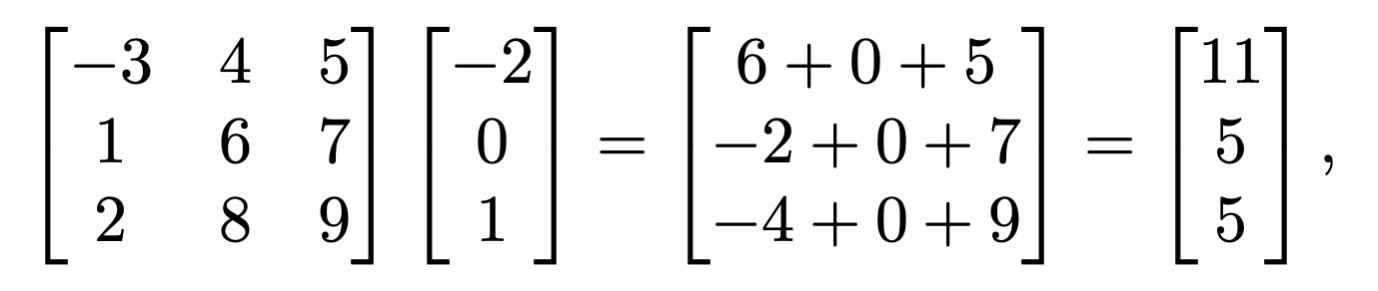
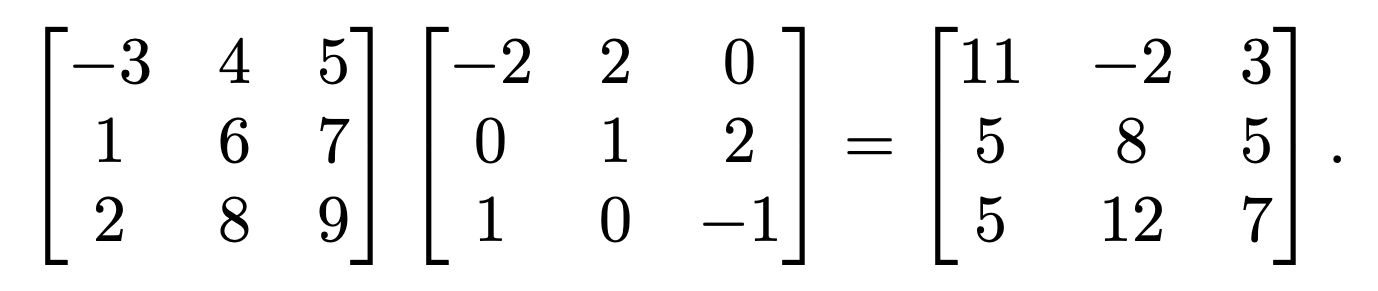
行列の役割：オブジェクトの編集
さて、ベクトルで座標を表すことにしましたが、行列はどんな役割を担うのでしょうか。
オブジェクトは複数の点から出来ていることを思い出しましょう。
そして、行列を掛けると、その点たちの座標が変化します。
ということは、行列を掛けることで、オブジェクトを編集することができるのです。
拡大・縮小
下の形の行列を掛けると、オブジェクトの拡大・縮小が行えます。
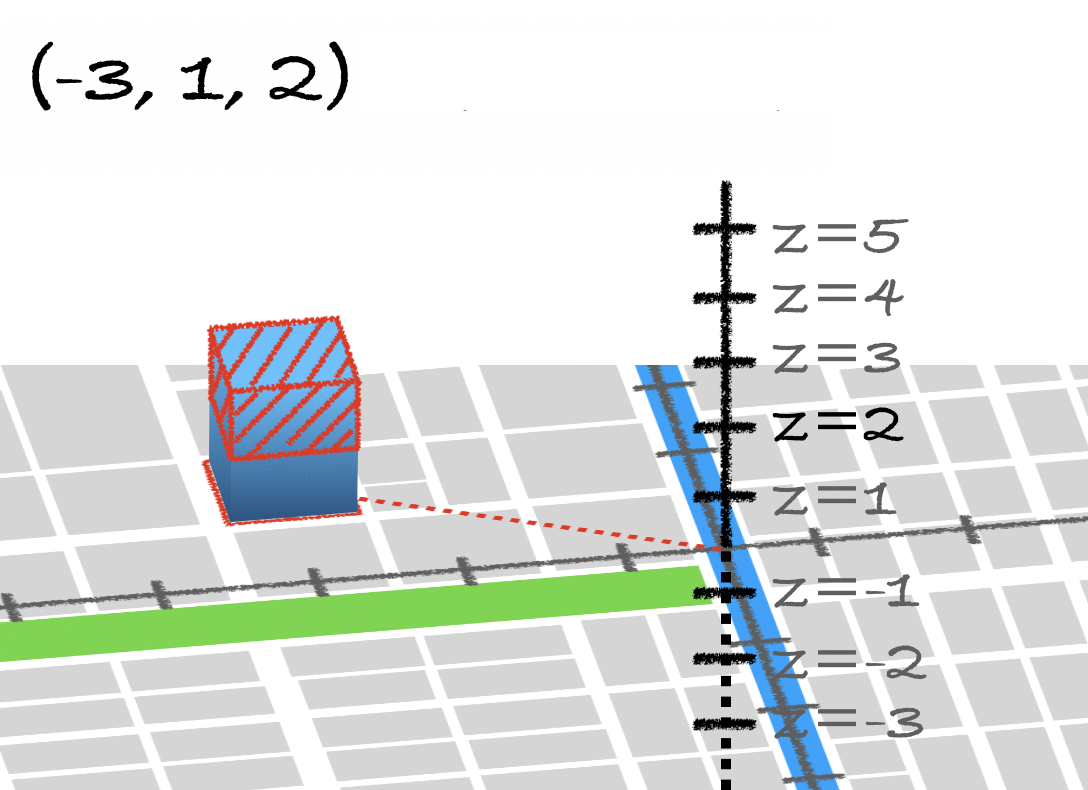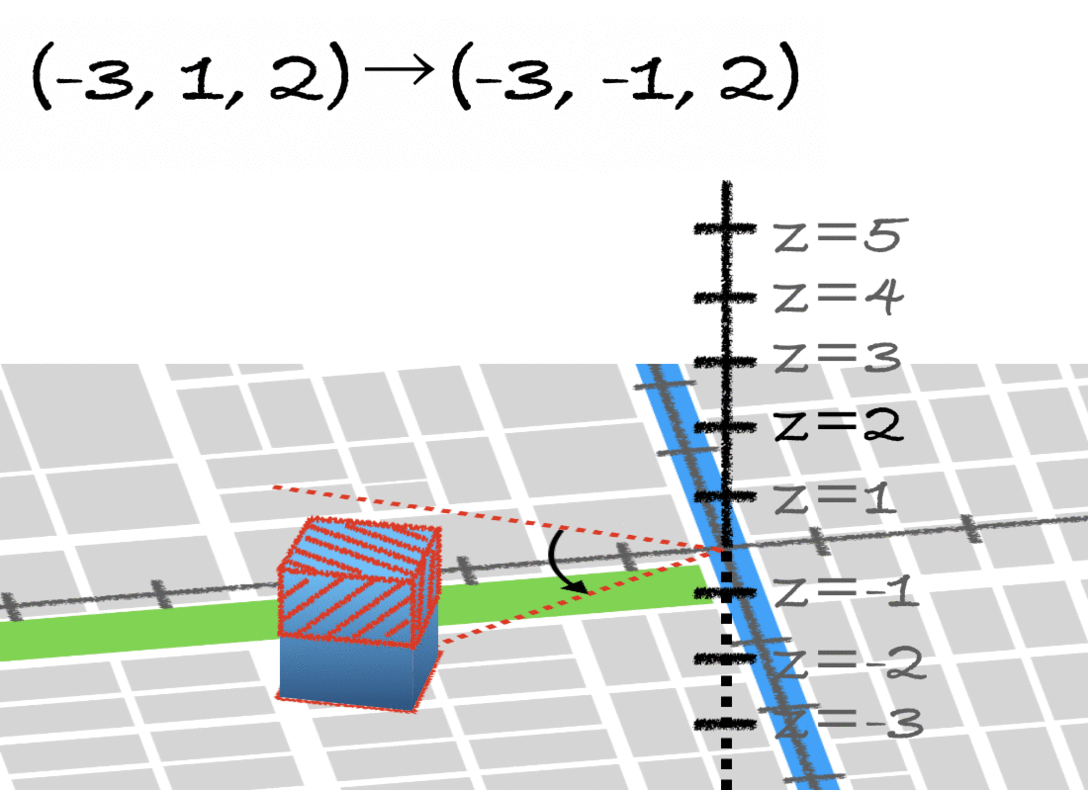
回転
下の形の行列を掛けると、オブジェクトの回転が行えます。
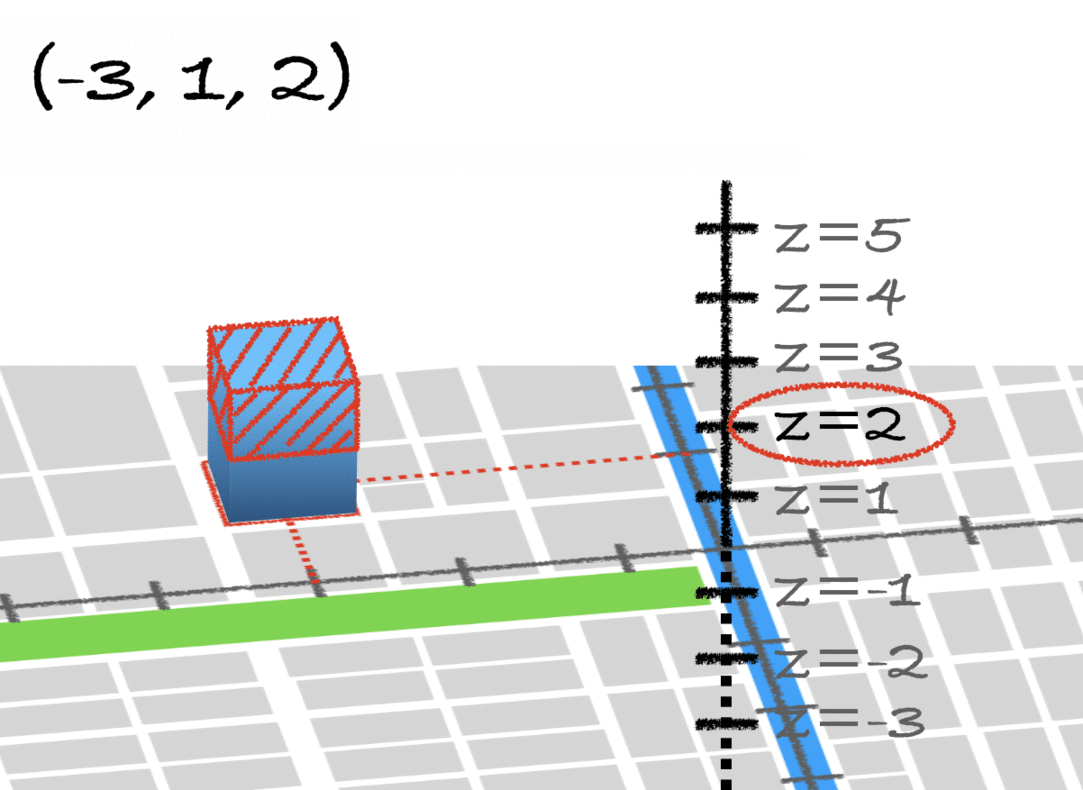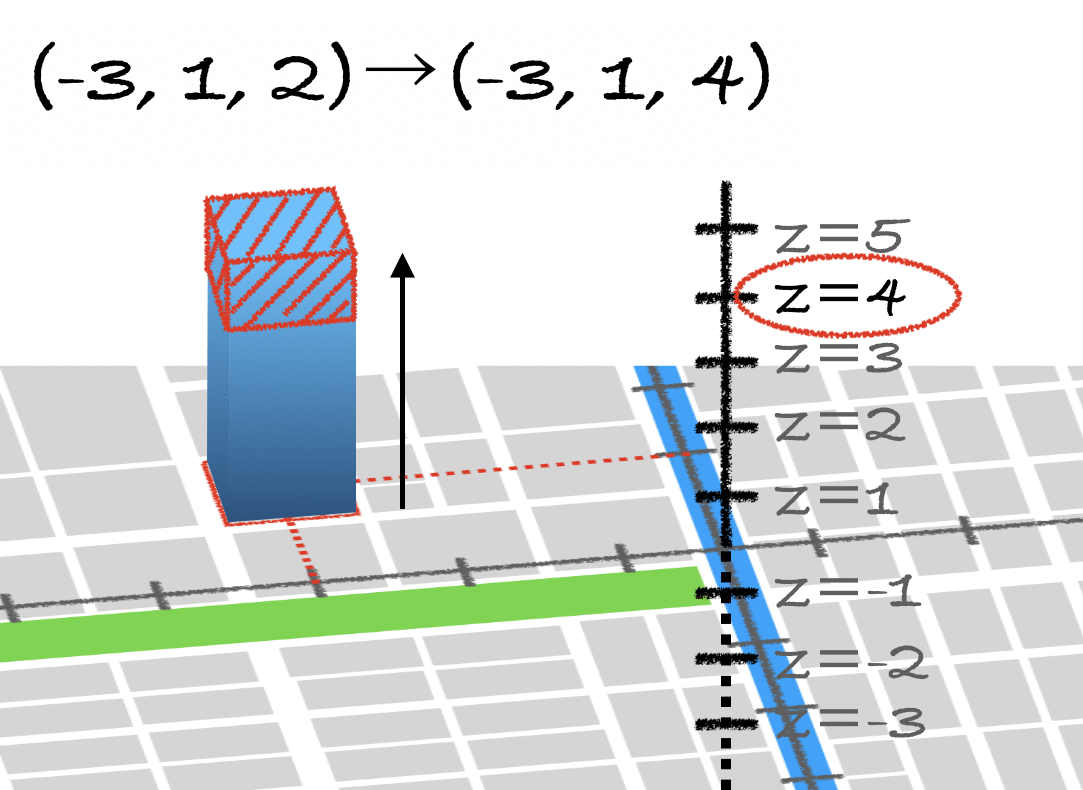
平行移動…？
上の2種類の行列を組み合わせると、オブジェクトを自由に編集できそうに思えます。
しかし、どう頑張っても平行移動ができないことに気付くはずです。
そこで登場するのが、4番目の座標Wを持つ同次座標系です。
※行列ついてもっと知りたい方には、こちらの本がオススメです。
同次座標系：Wの正体
同次座標（X, Y, Z, W）とこれまでの直交座標（x, y, z）は、次のような関係式で結びついています。
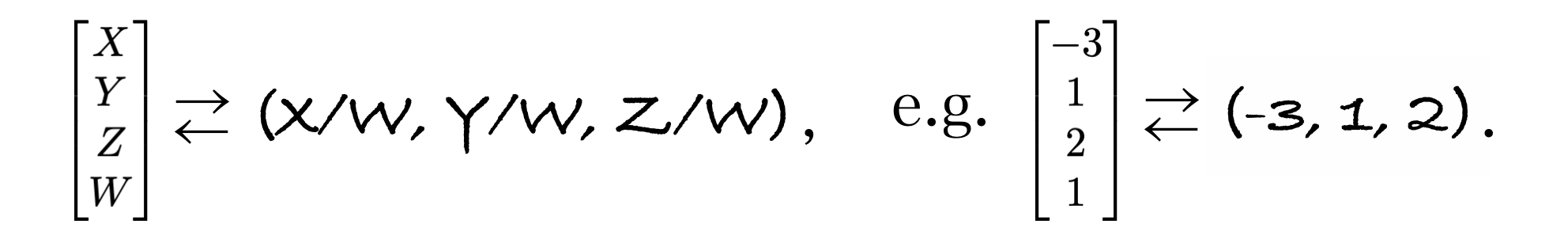
4番目の座標Wのおかげで、下の形の行列を掛けると、オブジェクトの平行移動が行えます。
ここまでをまとめると、同次座標系の導入によって、行列の掛け算という共通の操作で、オブジェクトを自由自在に編集できるようになりました。
つまり、コンピュータ上での計算効率が上がるということです。
また、W→0とすると無限遠点も含めて扱えることも、同次座標系の恩恵の1つです。
CGにおける様々な座標系
UnityをはじめとするCGでは、下に挙げる複数の座標系が用いられています。
そして、そうした座標系の間を橋渡しする方法こそ、まさに行列の掛け算と同次座標系なのです。拡大・縮小、回転、平行移動を組み合わせることで、夫々の間を行き来することができます。
あなたがUnity上でオブジェクトを操作した時、裏側ではこうした座標変換が何度も行われます。同次座標系の恩恵がそこで活かされるわけです。
ローカル座標系
オブジェクトを原点に取った座標系です。オブジェクトを構成する点同士の相対的な位置関係を表すのに用いられます。
ワールド座標系
全オブジェクトで共通の座標系です。これまでの図説で用いていたものです。オブジェクト同士の相対的な位置関係を表すのに用いられます。
ビュー座標系
カメラを原点に取った座標系です。カメラとオブジェクトとの相対的な位置関係を表すのに用いられます。
クリップ座標系
クリップ空間における座標系です。ワールドが実際にスクリーン上でどう見えるかを表すのに用いられます。
※補足： オブジェクトは3次元空間に配置されているので、スクリーン上に描画する際には奥行きを考慮しなければなりません。つまり、手前にあるものは大きく、奥にあるものは小さく描かなければならないのです。こうした操作は、カメラに映る範囲（Fig. 9で白い実線で囲われた立体の部分）を立方体に変形することで実現されます。ここで得られたクリップ空間（立方体状）における座標系が、プロジェクション座標系です。また、この変形の過程で、4番目の座標Wはカメラに映る範囲を切り取るのに用いられます。
スクリーン座標系
スクリーン上での座標系です。像同士の相対的な位置関係を表すのに用いられます。ビュー座標からクリップ座標を経由して得ることができます。
※おまけ：UV座標系
テクスチャ上での座標系です。シェーダでは、ローカル座標とUV座標とを結びつけることで、オブジェクト（3次元）にテクスチャ（2次元）を貼っています。
まとめ
以上、CGにおける座標系を徹底的に紐解いてみました。
同次座標系を用いれば、行列の掛け算という共通の操作で、オブジェクトを自由自在に編集できることがお分かり頂けたと思います。
今回は少し難しい内容でしたが、これらを理解していなければCGができない訳ではありません。自分の腑に落ちるまで、時間をかけて何度も何度も考えてみましょう。
それでは、楽しいXR開発を！
この記事はいかがでしたか？
もし「参考になった」「面白かった」という場合は、応援シェアお願いします！
